DDPM学习笔记
DDPM(Denoising Diffusion Probabilistic Models),是在2020年Jonathan Ho,Ajay Jain,Pieter Abbeel三位作者发表的论文Denoising Diffusion Probabilistic Models中提出的由随机噪声生成图片的模型,效果非常良好。但论文中有大量的概统内容,需要一定的数学基础。本文旨在与梳理复杂的公式,提取出其中了解代码所必需的内容
框架一览
DDPM大体可以分为两部分,加噪和去噪部分。其中加噪过程对应着训练过程,去噪过程对应着生成图片的过程。
加噪过程主体由两个模块组成:对图像进行不断加噪的部分和用加噪得到的结果进行训练的网络部分
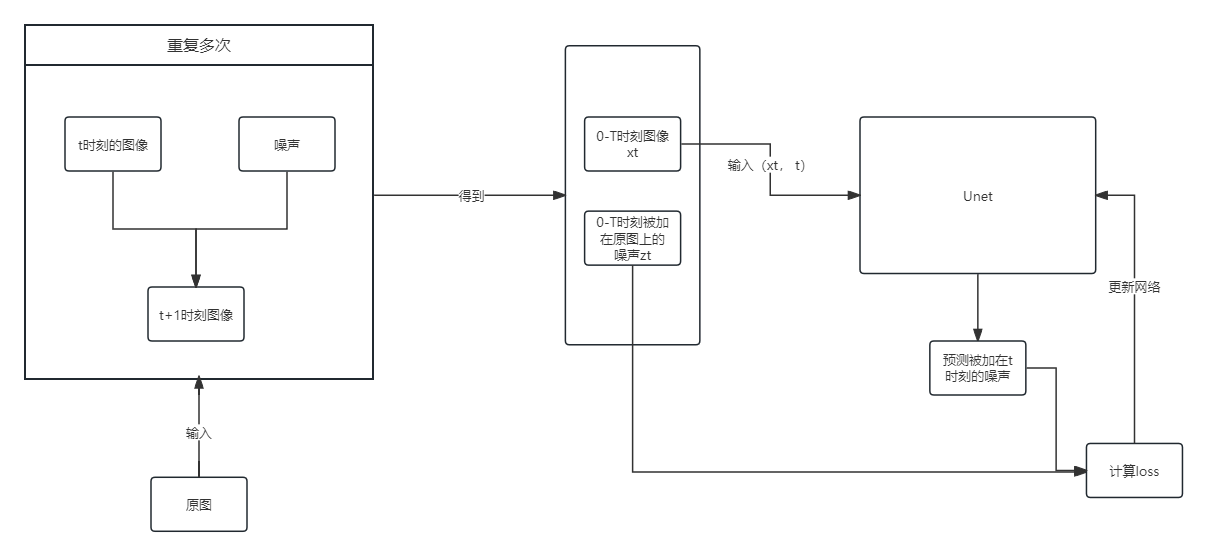
从上图可知,需要在模块之外进行传递的主要参数有:
- 输入加噪模块的原图$x_0$
- 从加噪模块输出,同时作为网络输入的$x_t$和时间标记t
- 从加噪模块输出,同时作为计算loss使用的每个时刻的噪声$z_t$
而去噪部分则是将一张噪声图片投入到网络中,和预测的噪声多次做减法,得到原图的过程
前向过程
数学推导
由于作者太菜本文主旨是辅助读者梳理为了手搓ddpm你需要了解的公式,因此这里我不会列出所有的推导公式
我们的目标是给$x_0$加上随机生成的噪声总共T次,每次加的噪声记为$z_t$。虽然是如此描述的,但我们加噪过程并不是简单的$x_{t+1}=x_t+z_t$。我们的模型是扩散(Diffusion)模型,因此,我们需要一个“扩散”的过程。即,我们用一个参数去控制每次加噪时噪声的占比,使得噪声是渐渐在原图上"浮现"出来。实际上我们单次加噪的模型如下:
$$ x_t = \sqrt{1-\beta_{t}}x_{t-1}+\sqrt{\beta_t}z_t, z_t\sim{N(0, I)} $$其中$\beta$即是上文中曾提到过的用来控制加噪时噪声占比的参数。同理,$x_{t-1}$也可以写成关于$x_{t-2}, z_{t-1}, \beta_{t-1}$的形式。
$$ x_{t-1} = \sqrt{1-\beta_{t-1}}x_{t-2}+\sqrt{\beta_{t-1}}z_{t-1}, z_{t-1}\sim{N(0, I)} $$我们直接带入上式。
$$ x_{t} = \sqrt{1-\beta_{t}}(\sqrt{1-\beta_{t-1}}x_{t-2}+\sqrt{\beta_{t-1}}z_{t-1})+\sqrt{\beta_t}z_t \\ = \sqrt{(1-\beta_{t})(1-\beta_{t-1})}x_{t-2}+\sqrt{(1-\beta_{t})\beta_{t-1}}z_{t-1}+\sqrt{\beta_t}z_t $$为了表达的更简便一些,我们设$\alpha_t = 1 - \beta_t$,那么上式子可以写成;
$$ x_t = \sqrt{\alpha_{t}\alpha_{t-1}}x_{t-2}+\sqrt{\alpha_t\beta_{t-1}}z_{t-1}+\sqrt{\beta_t}z_t $$迭代展开:
$$ x_t = \sqrt{\alpha_1\alpha_2\alpha_3...\alpha_t}x_0+\sqrt{\beta_t}z_t+\sqrt{\beta_{t-1}\alpha_t}z_{t-1}+\sqrt{\beta_{t-2}\alpha_{t-1}\alpha_{t}}z_{t-2}+...+\sqrt{\beta_1\alpha_2\alpha_3...\alpha_t}z_1 $$写的更抽象一点:
$$ x_t = \sqrt{\prod_{i = 1}^{t}\alpha_i}x_0+\sum_{i = 1}^{t-1}{\sqrt{(\beta_i\prod_{j=i+1}^{t}\alpha_j)}z_{i}}+\sqrt{\beta_t}z_t $$进一步简化公式,我们设$\overline\alpha=\prod_{i = 1}^{t}\alpha_i,\overline\beta = 1-\overline\alpha$。由于$z_1-z_t$都满足标准正态分布,我们可以直接将式子视为:
$$ x_t = \sqrt{\overline\alpha_t}x_0+\sqrt{\overline\beta_t}\overline{z}_t, \ \ \overline{z}_t\sim{N(0, I)} $$或者写成概率分布的形式:
$$ q(x_t|x_0) = N(x_t;\sqrt{\overline\alpha_t}x_0,(1-\overline\alpha_t)I) $$即,我们可以将其视为,$x_t$是直接由$x_0$一步加噪而来
代码部分
pass
反向过程
数学推导
首先我们需要明确反向过程究竟在做什么。反向过程中,我们需要从一张随机生成的噪声图像中逐渐恢复出一张完好的图像。在生成过程中,我们为数不多拥有的,就是随机生成的图像$x_T$和由网络预测而来的噪声$\overline z_t$,和生成时每一个时刻对应的$\alpha$与$\overline\alpha$。而我们最终目标就是将$q(x_{t-1}|x_t)$写成仅与这几者相关的形式。我们从最基本的后验概率模型出发:
$$ q(x_{t-1}|x_t) = \frac{q(x_t|x_{t-1})q(x_{t-1})}{q(x_t)} $$这个形式并不是我们想要的,我们想要右边几项更细节的表达。实际上,右边的这几项在前向的过程中都已经被计算过了。我们只需要将其写成有关$x_0$的形式:
$$ q(x_t|x_{t-1}, x_0) = \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z_t \sim{N(x_{t};\sqrt{\alpha_t}x_{t-1},(1-\alpha)I)}\\ q(x_t|x_0) = \sqrt{\overline\alpha_t}x_{0}+\sqrt{1-\overline\alpha_t}\overline{z}_t \sim{N(x_t;\sqrt{\overline\alpha_t}x_0,(1-\overline\alpha_t)I)}\\ q(x_{t-1}|x_0) = \sqrt{\overline\alpha_{t-1}}x_{0}+\sqrt{1-\overline\alpha_{t-1}}\overline{z}_{t-1} \sim{N(x_{t-1};\sqrt{\overline\alpha_{t-1}t}x_0,(1-\overline\alpha_{t-1})I)} $$而我们又知道高斯分布的公式:
$$ q(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \sim N(\mu,\sigma^2) $$我们将上述3式写成标准高斯分布,并带回表达式化简(这里略去数学证明),可以解得:
$$ q(x_{t-1}|x_t,x_0)=\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{1-\alpha_t}{\sqrt{1-\overline\alpha_t}}\overline{z}_t)+\sqrt{\frac{1-\overline{\alpha}_{t-1}}{1-\overline\alpha_t}(1-\alpha_t)} \\ \sim N(x_{t-1};\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{1-\alpha_t}{\sqrt{1-\overline\alpha_t}}\overline{z}_t),\frac{1-\overline{\alpha}_{t-1}}{1-\overline\alpha_t}(1-\alpha_t)I) $$通过上式,我们就可以用为数不多拥有的信息求出$x_{t-1}$,不断重复这个步骤,我们就能推断出$x_0$